就我个人而言,之前系统学过统计的机会不多,所以决定重新梳理一遍,并多向下挖一点,为后续的 IT 学习打基础。本文介绍数据集的一些基本要素与常见度量。
表达形式
数据集是一个抽象概念,不能直接观察或分析,需要先转为具体的表达形式。
列表/表格
最直接的方法是把数据逐项列出来。
| index | value |
|---|---|
| 1 | 60 |
| 2 | 65 |
| 3 | 67 |
| 4 | 67 |
条形图
当数据量较大时,条形图能展示各项及其出现频次。
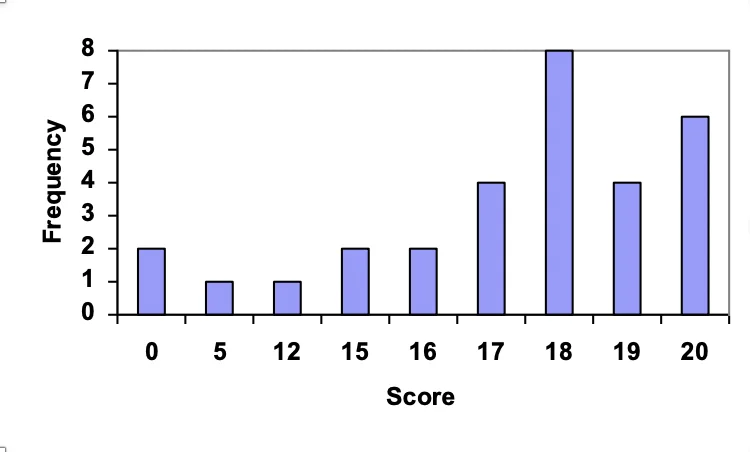
饼图
饼图可以直观展示各项所占比例。如果关注占比,用饼图更合适。
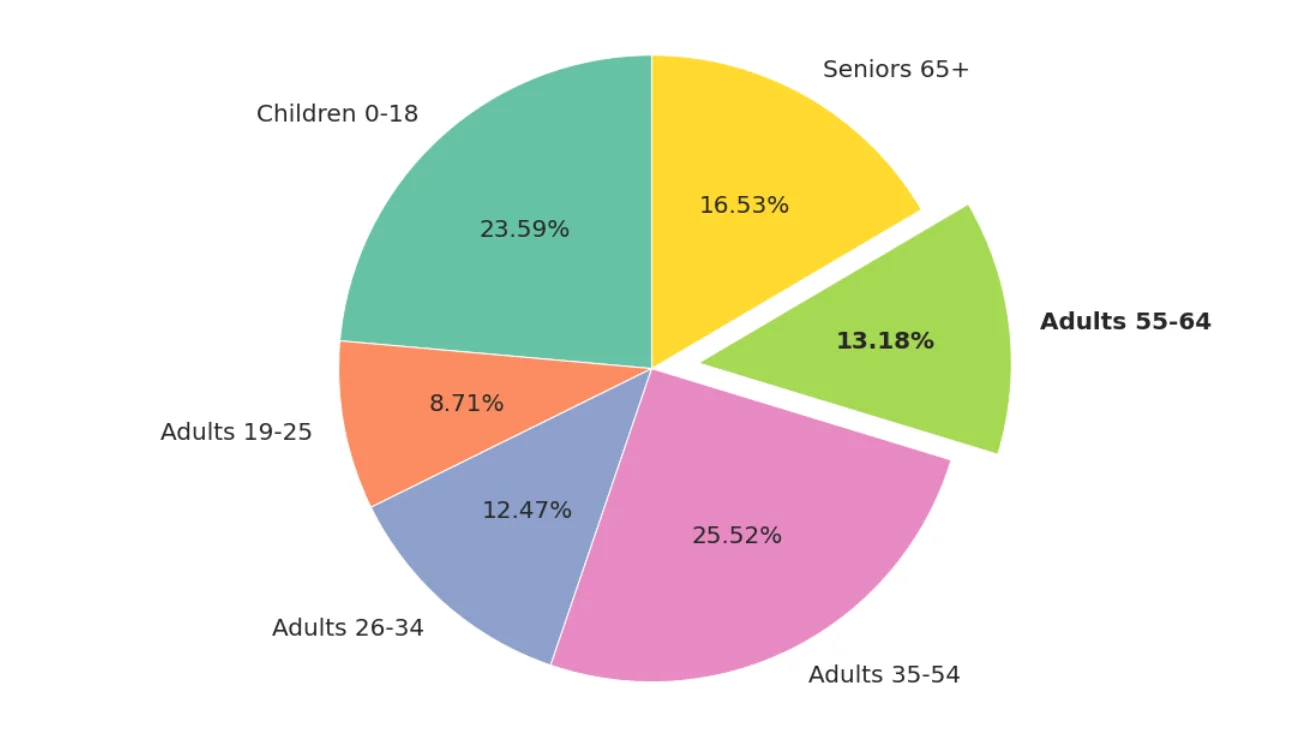
数据的“中间”
统计通常从“中心趋势”入手。常见的三个指标是:均值、中位数、众数。
均值(Mean)
即平均数:
$$ \bar{x} = \frac{x1+x2+…+xn}{n} $$
例:数据集 {1,2,3,5,6,6,7} $$ \bar{x} = \frac{1+2+3+5+6+6+7}{7} = 4.285… $$
中位数(Median)
将数据排序,取正中间值;若数量为偶数,取中间两项的平均。
数据集 {1,2,3,5,6,6,7} 的中位数是 5。
数据集 {1,2,3,5,6,7} 的中位数是 (3+5)/2 = 4。
众数(Mode)
出现次数最多的数。
数据集 {1,2,3,5,6,6,7} 的众数是 6。
数据的分布
即使两个数据集的均值/中位数/众数一致,它们也可能差异很大——因为分布不同。下面给出三个常见的分布度量。
极差(Range)
描述数据取值范围:
$$ Range = max - min $$
标准差(Standard Deviation)
衡量数据相对均值的离散程度。标准差越大,离散越大。
$$ \sigma = \frac{1}{n-1} \sum_{i=1}^{n}(x_i - \bar{x})^2 $$
重要:如果两个数据集所描述的对象不同,标准差不能直接比较!
例:数据集 1 是一天内的气温,标准差为 20;数据集 2 是老师的工资,标准差为 100。直观看 100 大于 20,但常识告诉我们:一天内气温相差 10℃ 已经很大,而工资差 100 并不大。因此,描述对象不同,标准差不可直接对比。
Z 分数(Z-score)
衡量某个点距离均值有多少个“标准差”:
$$ z = \frac{x-\bar{x}}{\sigma} $$
若数据满足正态分布:
1σ:约 68% 的数据落在均值 ±1σ 范围内。
2σ:约 95% 的数据落在均值 ±2σ 范围内。
3σ:约 99.7% 的数据落在均值 ±3σ 范围内,常用来识别“异常值”。
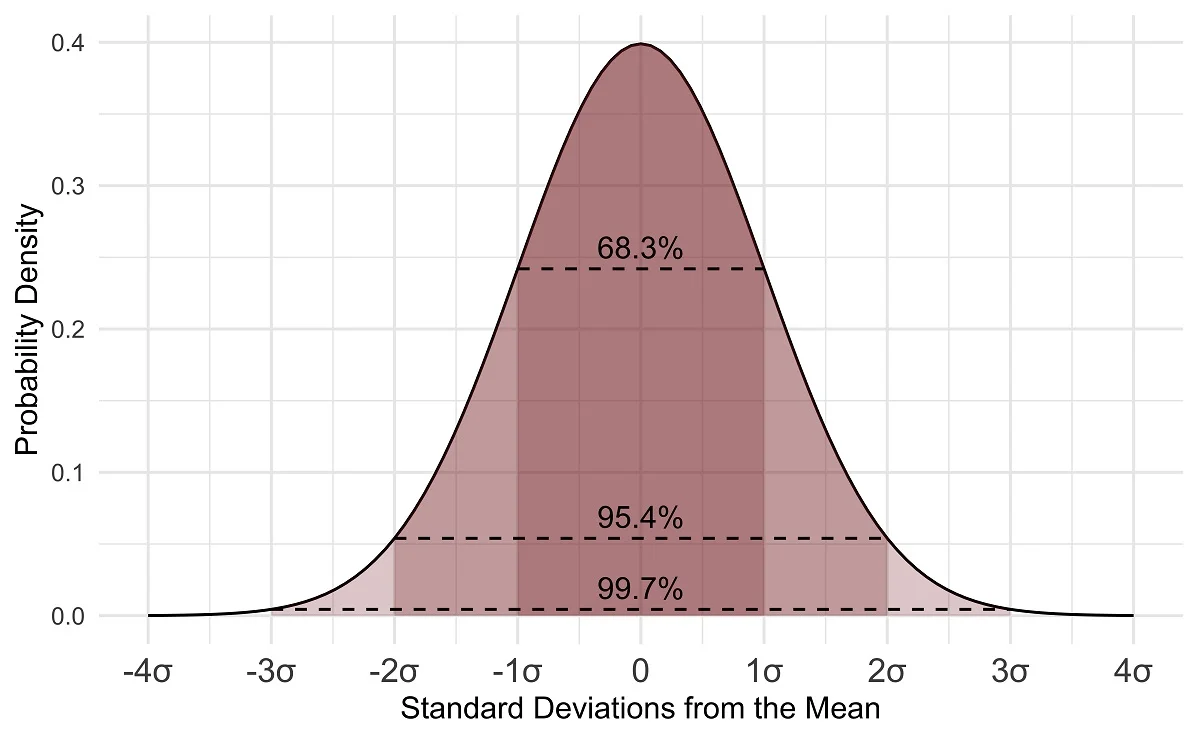
重要:异常值并不等于“应该被忽略”。事实上并没有严格定义哪些是异常值、如何处理它们。异常值可能蕴藏事实或趋势,因此需要谨慎对待。
