递归与汉诺塔：用归纳法写程序

汉诺塔是练习递归思维的经典问题。本文尝试用更直白的方式解释递归与汉诺塔，加深自己的理解。

如何理解递归

递归的本质是：把问题不断缩小，直到落到「基本情况」。递归难理解，是因为人脑没法像计算机一样跟踪深层调用链；一复杂就容易迷失在步骤里、前功尽弃，久而久之丧失信心。最好的办法是：相信你写的递归是能工作的，不要硬在脑内把每一步都「跑」一遍。

递归的前提

当问题规模较大、直接解不方便时，可以考虑递归。但需满足：

能拆成若干更小的同类型子问题，且子问题之间相对独立；
具备清晰的「基本情况/终止条件」，否则会无限递归。

如何搭建递归

一个递归函数通常包含 4 个部分：函数定义、基本情况、递归调用、结果返回。设计递归算法，就是明确这 4 件事。

函数定义

递归函数会调用自身，参数要能支撑两件事：完成本层职责、记录递归进度。以斐波那契为例：

1
2
3
4


// n 表示第 n 项
function fibonacci(n){
  // TBD
}

斐波那契的第 n 项由前两项之和决定，n 同时也是进度指示器，无需额外参数。

基本情况

把问题缩小，终会落到最小规模，即基本情况。斐波那契中，第 1、2 项已知：

1
2
3
4
5


function fibonacci(n){
  if (n === 1) return 0; // 第一项
  if (n === 2) return 1; // 第二项
  // TBD
}

递归调用

设 f(n) 为第 n 项，有递推式 f(n)=f(n-1)+f(n-2)。这把问题拆成两个更小的同类问题：

1
2
3
4
5
6


function fibonacci(n){
  if (n === 1) return 0;
  if (n === 2) return 1;
  const ans = fibonacci(n-1) + fibonacci(n-2);
  // TBD
}

再次强调：别在脑中追踪整条递归链。站在当前这一层，只关心本层做了什么，并相信子调用会返回正确结果。

返回结果

本层的职责是算出第 n 项并把它返回，供上一层使用：

1
2
3
4
5


function fibonacci(n){
  if (n === 1) return 0;
  if (n === 2) return 1;
  return fibonacci(n-1) + fibonacci(n-2);
}

这也形成了尾递归可优化的形态：当递归调用是函数的最后一步时，很多语言可将其优化为迭代，降低栈开销。

汉诺塔问题

汉诺塔是递归的经典练习。随圆盘数量增加，步骤迅速增长。

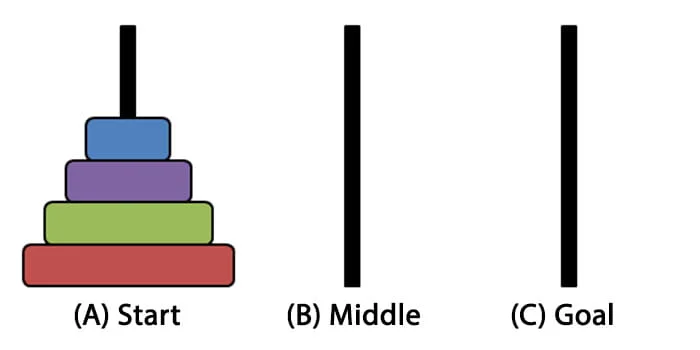
Hanota

问题分析

若只有 1 个盘，直接把它从起点挪到终点即可。2 个盘时：先把小盘移到中间，再把大盘移到终点，最后把小盘移到大盘上。3 个以上看起来就复杂了。

3 盘示意

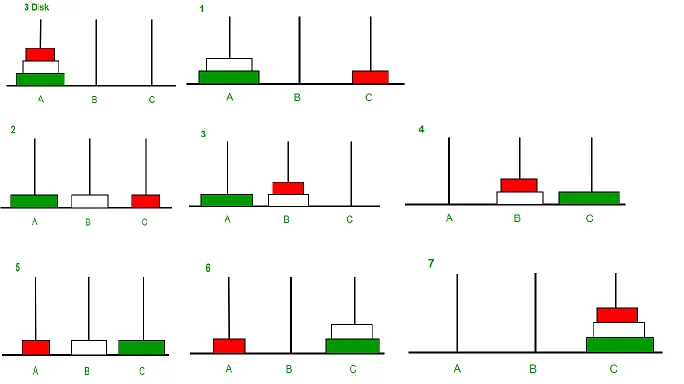
两条关键事实：

小盘可以放在大盘上，因此「一堆盘叠在最大盘上」与「只剩最大盘」的塔，对上层而言等价，可用于缩小问题规模；
初始时最大盘在最底部，意味着我们可以先忽略它，先处理其上的 n-1 个小盘。

据此，整体可以拆为三步：

把 n-1 个小盘从起点移到中转塔；
把第 n 个（最大）盘从起点移到终点；
把 n-1 个小盘从中转塔移到终点。

第 1、2 步的目的，是让最大盘到位，从而把规模从 n 缩到 n-1。虽然「一次性搬运 n-1 个盘」在现实中不可行，但在递归的抽象里，我们把它当作「子问题」来解即可。

代码草图

用三个数组表示三根柱子 src/buf/tar，用参数 i 表示当前要处理的盘数：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19


function move(data, src, tar) {
  const pan = data[src].pop();
  data[tar].push(pan);
  console.log(`move ${pan} from ${src} to ${tar}`);
}

function dfs(i, data, src, buf, tar) {
  if (i === 1) { move(data, src, tar); return; }
  dfs(i - 1, data, src, tar, buf);
  move(data, src, tar);
  dfs(i - 1, data, buf, src, tar);
}

function hanota(data) {
  dfs(data.src.length, data, 'src', 'buf', 'tar');
}

let data = { src: [10,9,8,7,6,5,4,3,2,1], buf: [], tar: [] };
hanota(data);

参考

递归中的逆向思维
如何治疗晕递归?
汉诺塔问题