Hanota is a classic programming question that is a really good cutting point for forming recursive thinking mode. In this post, I will try to explain recursion and Hanota problem in my own words to enhance my understanding.

# How to Understand Recursion

The essence of recursion is scaling down the problem size until it reaches a base case. The reason why recursion is hard to grasp is because our brain cannot follow the execution chain of recursion as computers do. Once the logic becomes complex, we might forget which step we are at and lose the progress, inevitably, we need to start over. After a couple of attempts, we might lose the confidence and patience, eventually leading to giving up. So the best way to understand it is to trust your recursion can function.

# Prerequisites of Recursion

Usually, when the problem size is quite large for solving it directly, recursion might be a possible solution. You can only apply recursion to your task only if the task

1. can be split into smaller chunks and they are independent to each other.
2. the base case or the terminate condition is clear. (Otherwise the recursion would be endless)

# How to Build Recursion

A normal recursion function consists of 4 parts: function definition, base case/terminate condition, recursive calling, result returning. To design an appropriate recursive algorithm is to determine how to implement these parts.

# Function Definition

Recursive function is a special function that calls itself and the most important part in this step is to determine the argument list. Not only the argument list needs to provide all arguments needed by the function to fulfil its responsibility, also records the progress of the recursion. For example, if we want to calculate the n-th item of fibonacci list, the definition should be like:

1
2
3
4

// n indicates the n-th item of fibonacci list
function fibonacci(n){
    // TBD
}

The item of fibonacci list is always the sum of the previous two items, and n also indicates the progress of the recursion, so there’s no extra argument needed.

# Base Case

As mentioned above, recursion scales the problem size down to simplify the issue. The base case is the case when the problem size is minimum. Based on the prerequisite 2, the base case should be clear, in other words, we know when the recursion should stop. We still use the case of fibonacci: the first and second items are 0 and 1, while the calculation starts from 3rd item.

1
2
3
4
5
6
7
8

// n indicates the n-th item of fibonacci list
function fibonacci(n){
    // the first item of fibonacci list is 0
    if (n == 1) return 0;
    // the second item of fibonacci list is 1
    else if (n == 2) return 1;
    // TBD
}

When the problem size shrinks to 2 or 1, the recursion will stop.

# Recursive Calling

Assuming f(n) is the n-th item of fibonacci list, we can get the formula f(n) = f(n-1) + f(n-2). As you can see, the problem has been split into two sub-issues, so the problem size has been reduced. According to the terminate condition we defined in the last step, once the problem has been scale down to a specific size, the known answer can be used to infer the unknown.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

// n indicates the n-th item of fibonacci list
function fibonacci(n){
    // the first item of fibonacci list is 0
    if (n == 1) return 0;
    // the second item of fibonacci list is 1
    else if (n == 2) return 1;
    // According to the recurrence formula
    const ans = fibonacci(n-1) + fibonacci(n-2);
    // TBD
}

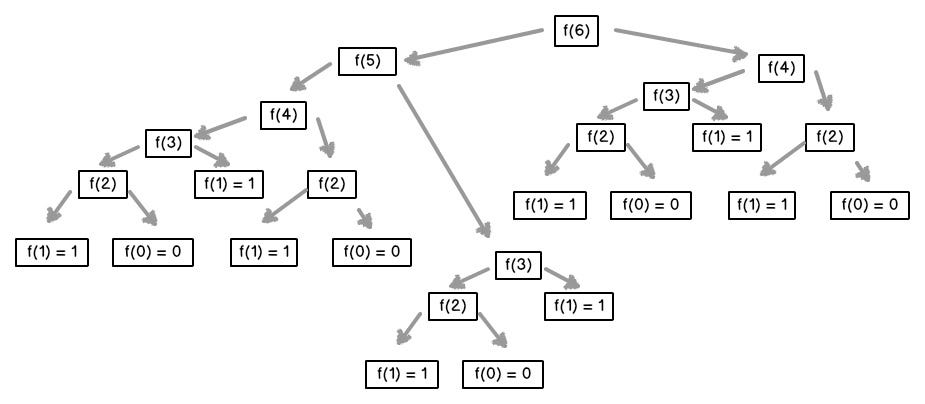
There is a critical thing worth to be noted again: Don’t try to follow the recursion chain in your mind. In contrast, you should believe the recurrence formula can work properly. For each layer of recursion, you should only consider what has been done in this level.

# Return the Result

In the term of our expectation/assumption, each time we call the function fibonacci, it would calculate the value of n-th item of fibonacci list. In this step, the only step we need to do is to return the result of this layer, which provides the basis of upper recursion.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

// n indicates the n-th item of fibonacci list
function fibonacci(n){
    // the first item of fibonacci list is 0
    if (n == 1) return 0;
    // the second item of fibonacci list is 1
    else if (n == 2) return 1;
    // According to the recurrence formula
    const ans = fibonacci(n-1) + fibonacci(n-2);
    // return the result to the upper recursion
    return ans;
}

Tail recursion optimization is a technique that can optimize the cost of memory and stack call. When the recursion call is the last step of the recursion function, recursion can be turned into iteration. This technique has been supported in many programming language, and applying it in codes is always a good practice. In the case above, tail recursion optimization can be easily performed.

1
2
3
4
5
6
7
8
9

// n indicates the n-th item of fibonacci list
function fibonacci(n){
    // the first item of fibonacci list is 0
    if (n == 1) return 0;
    // the second item of fibonacci list is 1
    else if (n == 2) return 1;
    // According to the recurrence formula
    return fibonacci(n-1) + fibonacci(n-2);
}

# Hanota Problem

Hanota problem is a classic problem can be solved by recursions. As the number of disk goes up, the problem is increasingly complex (more steps to finish).

# Problem Analysis

To solve this problem using coding, problem analysis is always the first step. Of course, if there is only one disk, that is the simplest case because you can move it to the goal tower directly. What if there are two disks? Moving the smaller one to the middle tower, Moving the larger one to the target tower and moving the smaller from middle to goal tower. You can also finish in 3 steps. Then you find the problem is not easy after 3 disks.

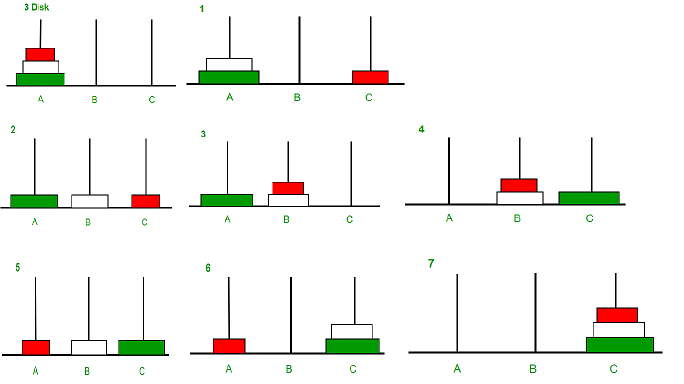
Emm, it looks complicated and not relavant to previous cases. No worries, there are two truth from the game rules:

1. The smaller disk can always be putted on the larger disk, so all disks can be on the largest disk, which means a tower with the largest disk only is the same as empty tower. This can help us reduce the problem size.
2. For the initial state, the largest disk is on the bottom of the start tower, so it allows us to ignore it at first.

Based on the two truths we found, the whole game can be split into three steps:

1. move n-1 disks from start to middle
2. move the n-th disks from start to goal
3. move n-1 disks from middle to goal

The first 2 steps are going to move the largest disk from start to goal, which can reduce the problem size as memtioned. Despite moving n-1 disks all together at once is impossible, that’s the job of recursion, so we just need to regard it as possible action.

# Function Definition

In this problem, we need to track the status of three tower, so we assign 3 variables src,buf,tar as the status of start, middle, goal towers. However, the status of start tower cannot be used as the indicator of problem size since its status is not change when moving disks, so we also need another variable i as the problem size.

# Base Case

In this problem, the base case is when only one disk exists.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

function hanota(i, src,buf,tar) {
    // when there is only 1 disk
    if (i == 1){
        // To simplify the problem
        // I will show the implementation below 
        // It will move the uppermost disk from src to tar
        move(src, tar);
        // work done, just return to finish
        return;
    }
    // TBD
}

# Recursive Calling

There are three recursive callings as mentioned above. When you move the n-1 disks from start to the goal tower, the problem size is n-1.

1
2
3
4
5
6
7
8
9

function hanota(i,src,buf,tar){
    if (i==1) {
        move(src,tar);
        return;
    }
    // move n-1 disks from start to middle
    // in this case, the goal tower is the role of buffer
    hanota(i-1, src, tar, buf);
}

Then move the largest disk from the start to the goal tower, which is quite simple.

1
2
3
4
5
6
7
8

function hanota(i,src,buf,tar){
    if (i==1) {
        move(src,tar);
        return;
    }
    hanota(i-1, src, tar, buf);
    move(src,tar);
}

finally, move n-1 disks from the middle to the goal tower, which is similar as step 1.

1
2
3
4
5
6
7
8
9

function hanota(i,src,buf,tar){
    if (i==1) {
        move(src,tar);
        return;
    }
    hanota(i-1, src, tar, buf);
    move(src,tar);
    hanota(i-1, buf, src, tar);
}

Since all operations manipulated src/buf/tar, so we don’t need to return anything to notify upper layer.

# The Code

To print the steps, I made some adjustment to the previous code.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

let data = {
    src: [10, 9, 8, 7, 6, 5, 4, 3, 2, 1],
    buf: [],
    tar: []
}

// move item from src to tar
function move(data, src, tar) {
    // get the uppermost item of src
    const pan = data[src].pop();
    // add it to the top of tar
    data[tar].push(pan);
    // print the operation
    console.log(`move ${pan} from ${src} to ${tar}`);
}

function hanota(data) {
    const src = "src";
    const buf = "buf";
    const tar = "tar";
    const i = data[src].length;
    dfs(i, data, src, buf, tar);
}

function dfs(i, data, src, buf, tar) {
    if (i == 1) {
        move(data, src, tar);
        return;
    }
    dfs(i - 1, data, src, tar, buf);
    move(data, src, tar);
    dfs(i - 1, data, buf, src, tar);
}

hanota(data);

# Reference

• 递归中的逆向思维
• 如何治疗晕递归?
• 汉诺塔问题